The Task

Implement the Drossel and Schwabl definition of the forest-fire model.

It is basically a 2D cellular automaton where each cell can be in three distinct states: empty, tree and burning, and evolves according to the following rules:

1. A burning cell turns into an empty cell,
2. A tree will burn if at least one heighbor is burning,
3. A tree ignites with probability f even if no neighbor is burning,
4. An empty space fills with a tree with probability p.

Neighborhood is the Moore neighborhood; boundary conditions are so that on the boundary the cells are always empty ("fixed" boundary condition).

At the beginning, populate the lattice with empty and tree cells according to a specific probability (e.g. a cell has the probability 0.5 to be a tree). Then, let the system evolve.

---

We solve this task graphically with help of the canvas.l library. In the end, it will look like this:

Parameters:

• "cell has tree" probability: 50 %
• Ignition probability f: 0.01 %
• "Empty space fills with tree" probability p: 1 %
• Number of cells: 480x360 = 172800

---

The simul.l library file

In cellular automata, the Moore neighborhood is defined on a two-dimensional square lattice and is composed of a central cell and the eight cells that surround it.

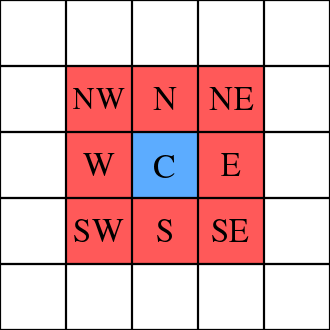
We can use the simul.l library for this purpose, which defines the functions grid, west, east, south and north in the namespace simul.

Let's load the libraries and functions:

(load "@lib/http.l" "@lib/xhtml.l" "@lib/form.l" "@lib/canvas.l" "@lib/simul.l") 
(import simul~grid simul~west simul~east simul~south simul~north)

---

First of all, we define the grid size *CanvasDX and *CanvasDY, go(), drawCanvas and a function called forest:

(setq *CanvasDX 480  *CanvasDY 360)

(de drawCanvas (Id Dly)
]

(de forest ()
   (and (app) *Port% (redirect (baseHRef) *SesId *Url))
   (action
      (html 0 "Forest Fire" "@lib.css" NIL
         (form NIL
] 

(de go()
   (server 8080 "!forest"))

---

Now we can define the grid *FireGrid by using the grid function from simul.l. We can return a random T/NIL value by calling (rand T).

(for Col (setq *FireGrid (grid *CanvasDX *CanvasDY))
   (for This Col
      (=: tree (rand T)) ) )

---

The *FireGrid object

This approach uses the convenient fact that the canvas "ID" can actually be an object. Let's pass the object *FireGrid to <canvas> and re-draw it every 40 milliseconds:

(<canvas> "$*FireGrid" *CanvasDX *CanvasDY)
(javascript NIL "onload=drawCanvas('$*FireGrid', 40)")

We define that the *FireGrid object has three attributes:

• tree, which is T if the tree is intact,
• burn, which is T if the tree is burning,
• next, which shows the status in the next iteration.

---

Now we define the drawCanvas function. In the first step, we iterate over every cell in *FireGrid and set the next attribute according to the following rules:

1. The tree is burning: next will be NIL.
2. The tree is intact:
   • next will be burn, if a neighbor tree is burning.
   • next will be burn with a probability of 0.1 % (ignition)
   • otherwise, next is tree.
3. The cell object s NIL: next is tree with a probability of 1 %, otherwise NIL.

(for Col *FireGrid
   (for This Col
      (=: next
         (cond
            ((: burn) NIL)
            ((: tree)
               (if
                  (or
                     (find  # Neighbor burning?
                        '((Dir) (get (Dir This) 'burn))
                        (quote
                           west east south north
                           ((X) (south (west X)))
                           ((X) (north (west X)))
                           ((X) (south (east X)))
                           ((X) (north (east X))) ) )
                     (=0 (rand 0 9999)) )
                  'burn
                  'tree ) )
            (T (and (=0 (rand 0 99)) 'tree)) ) ) ) )

---

Then we iterate over *FireGrid again, this time in order to set each cell to the value stored in next:

(for Col *FireGrid
   (for This Col
      (if (: next)
         (put This @ T)
         (=: burn)
         (=: tree) ) ) )

---

Drawing the canvas

Now that the new state of *FireGrid is defined, let's draw it:

• For each tree cell, we draw a green dot.
• For each burn cell, we draw a red dot.

We do this with the csDrawDots function, which does not directly map to a JavaScript function. Instead, we need to define a list of pixel positions which are rendered to the canvas with help of the JavaScript ctx.fillRect function. This is more efficient than defining each pixel in a loop.

We call csDrawDots two times: First for green pixels of size 1 (in x and y direction) to represent the trees, and then red pixels of size 3 to represent the fire.

(make
   (csClearRect 0 0 *CanvasDX *CanvasDY)
   (csFillStyle "green")
   (csDrawDots 1 1
      (make
         (for (X . Col) *FireGrid
            (for (Y . This) Col
               (and (: tree) (link X Y)) ) ) ) )
   (csFillStyle "red")
   (csDrawDots 3 3
      (make
         (for (X . Col) *FireGrid
            (for (Y . This) Col
               (and (: burn) (link X Y)) ) ) ) ) )

---

You can find the source code of the finished example here.

---

Sources

rosettacode.org/wiki/Forest_fire
en.wikipedia.org/wiki/Cellular_automaton
en.wikipedia.org/wiki/Moore_neighborhood