This task is actually not included in the Rosetta code, but still it is a quite frequent algorithmic task: How to find the optimal path between two nodes of a graph. In this post, we will show a brute-force solution using Pilog to get from A to B.
An alternative algorithm to solve this kind of task is using Dijkstra's algorithm. You can find an implementation here (only PicoLisp, not in Pilog).
Task description
Given a list of cities and the distances between each pair of cities, find the optimal route from city A to city B.
In this task, our salesman frequently needs to visit the following cities: Rheine, Münster, Onsabrück, Warendorf, Rheda, Bielefeld, Paderborn, Soest, Ahlen, Beckum, Rheda, Gütersloh. (Don't worry if you have never heard of some of those, I haven't either).
This is the distance information that we have:
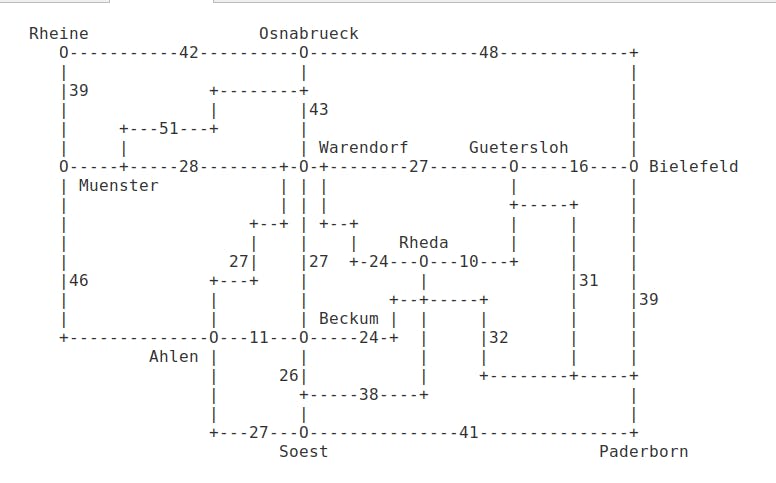
(be vect (Rheine Muenster 39))
(be vect (Rheine Osnabrueck 42))
(be vect (Muenster Osnabrueck 51))
(be vect (Warendorf Muenster 28))
...
In this example, we will first write an algorithm that finds all possible paths between city A and city B. After that we will find the minimum value using the PicoLisp mini function.
Creating the Graph functions
We are modeling our city model als simple undirected, weighted graph, where the distances are described by the vect predicate. The nodes are the cities, and the edges show the distance. "Undirected" means that we can travel in both directions. "Weighted" means that the edges are associated with a unit that can be used to optimize the route - in this case, the distance in kilometers.
Let's create a predicate edge that returns T if we have a vector between two cities @A and @B, and NIL if not.
(be edge (@A @B @N) (vect @A @B @N))
(be edge (@A @B @N) (vect @B @A @N))
Define the starting predicate path
Now we want to create all paths between two nodes. We define a predicate path with start @A, destination @B, path @P and cost @N:
(be path (@A @B @P @N))
where @P is a list of cities. Unfortunately we cannot work well with this definition because in order to implement our backtracking mechanism, it would be helpful to reflect the "middle" stations as well.
Therefore we define a "helper predicate" path1 and split the path @P in two parts: The list of cities required to reach a current stop (@L), and another list to reach from the current stop @A to the final destination @B.
(be path1 (@A @B @L (@A . @P) @N)
What is the connection between path and path1? For initialization, we are only considering the start and destination stop. Therefore @L is equal to the start stop (because we didn't move from there yet), and @P is equal to the remaining distance.
(be path (@A @B @P @N)
(path1 @A @B (@A) @P @N) )
Define the backtracking mechanism in helper predicate path1
Now we can define all the recursive logic in our helper predicate path1. First the base case @B = @A: If start and destination are equal, then our "up to point @A" travel list remains unchanged (= @L), and the "from @A to @B" travel list contains only one element: (@A). The travel cost is zero.
(be path1 (@A @A @L (@A) 0.
Now what if @A not equal to @B? In that case, we need to modify the path "from @A to @B" to (@A . @P): a list starting at @A with all stops until destination @B.
be path1 (@A @B @L (@A . @P ) @N)
Now how do we get from @A to @B? We need to check if there is any city @Z we can reach from @A. The following conditions need to be fulfilled:
- There is an edge between
@Aand@Zat cost@X, @Zis not on our path@Lyet. We check this with the built-in predicatemember.
In Pilog:
(be path1 (@A @B @L (@A . @P) @N)
(edge @A @Z @X)
(not (member @Z @L))
... )
Now we calculate our route from @Z to @B. Since we "increment" the starting point, we need to add it to the head of our travelling path @L.
(path1 @Z @B (@Z . @L) @P @Y)
In the "best case", @Zand @B are equal, which means we are calling the base case and exit the recursion.
Calculating the cost
The cost is simply the sum of the weighted graphs of the whole path. If we have travel cost of @X from A to Z, and @Y from Z to B, then in total our cost is @X+@Y. So let's set this sum to @N in the last step. This is our final predicate definition:
(be path1 (@A @A @L (@A) 0))
(be path1 (@A @B @L (@A . @P) @N)
(edge @A @Z @X)
(not (member @Z @L))
(path1 @Z @B (@Z . @L) @P @Y)
(^ @N (+ @X @Y)) )
Calling the function and finding the minimum
If we run a query like (? (path Bielefeld Muenster @P @N)), we will typically get more than one result. We can process the whole set of return values using the solve function:
(solve 'lst . prg) -> anyEvaluates a Pilog query and, returns the list of result sets. If
prgis given, it is executed for each result set, with all Pilog variables bound to their matching values, and returns a list of the results.
Like this:
(solve '(
@A 'Rheine
@B 'Muenster
(path @A @B @P @N) )
Now we want the optimal result, i.e. with the minimal cost (@N). In order to access it, let's store each result in a cons pair (cons @N @P) (a key-value pair stored in a cell with a value in CAR and CDR each). Read here if you don't know what a cell is.
Then we can find the minimum value using the mini function which applies a function to a list and returns the minimal value. In our case, we get back a list of cons pairs and we're looking for the minimum CAR value which we can get with car.
(mini car
(solve
'( <pilog query>
(cons @N @P) ) )
As last step, let's wrap everything into a function.
(de travel (A B)
(mini car
(solve
...
If we now start the program in debug mode: pil travel.l +, we can interact with it in the REPL:
: (travel 'Muenster 'Warendorf)
-> (28 Muenster Warendorf)
You can find the finished program here.
Sources
irasutoya.com/2014/07/blog-post_8691.html
software-lab.de/doc/index.html