Riddle 7: 10001st Prime

The Task

By listing the first six prime numbers: 2, 3, 5, 7, 11, and 13, we can see that the 6th prime is 13.

What is the 10.001st prime number?

This is a surprisingly tricky one, because the code should execute within one minute according to the Project Euler rules. I will present two easy approaches that are too slow, and a slightly more complicated one that works.

How to determine Prime Numbers

Prime numbers are only dividable by themselves and by 1. As naive approach we could test all numbers between 2 and N-1 if they are evenly dividable.

(de isPrime (N)
   (let Prime T
      (for I (- N 2)
         (when (=0 (% N (inc I)))
         (when (=0 (% N I))
            (setq Prime NIL) ) )
   Prime ) )

However, this code quickly gets very unefficient, as we need N-2 divisons per number. In order to calculate the 10.001st prime number, how many would that be?

According to online sources, the 10.000 prime is at around ~106.000. In other words, to test them all, we need more than 106.000! (faculty) calculation steps, which means 10^486650 steps (a 26497 digit number!).

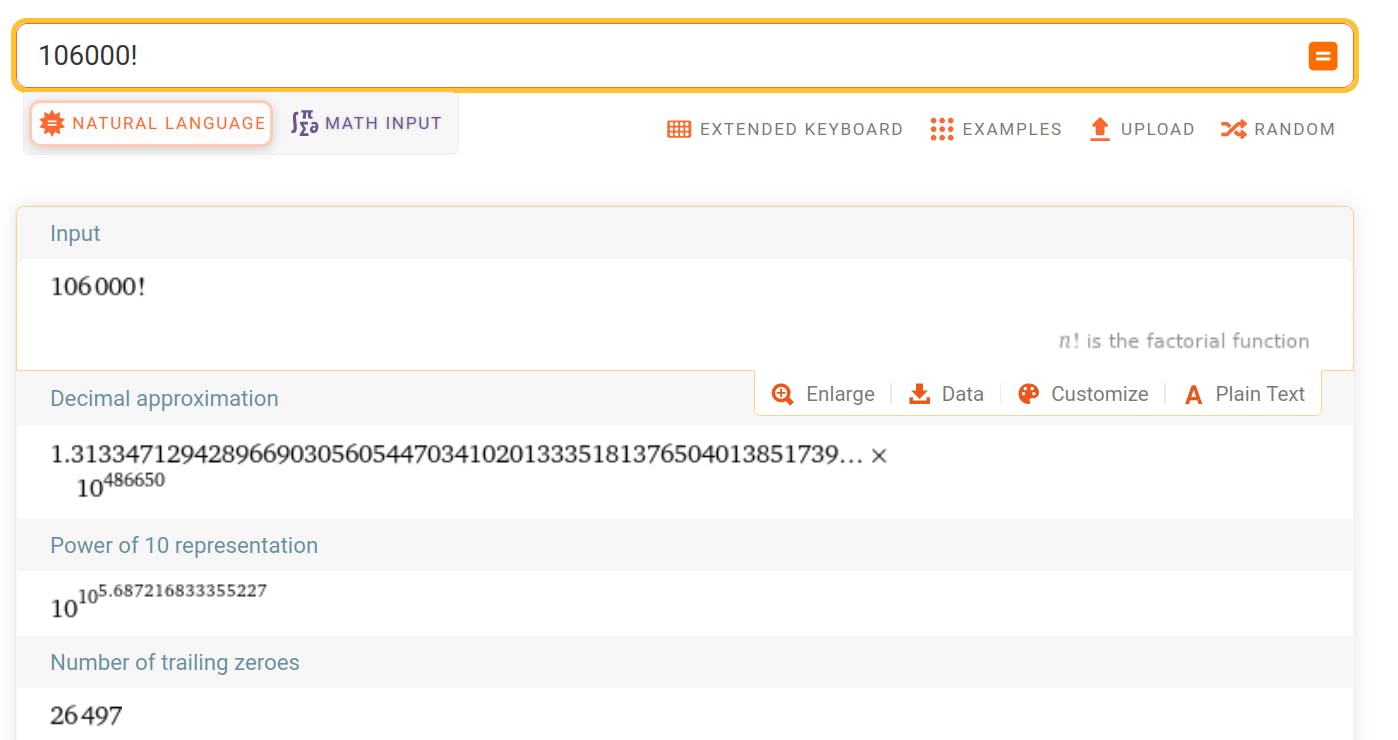
Since all Euler tasks are supposed to run within less than 60 seconds on a "normal" laptop, this is certainly not the way to go. Let's look for improvements.

The Sieve of Eratosthenes

Note: The following code is heavily inspired by the Rosetta Code submission for the Sieve of Eratosthenes.

The Sieve of Erosthenes is an algorithm to determine all prime numbers up to a given range. On Wikipedia, you can find a nice animation which illustrates how it works:

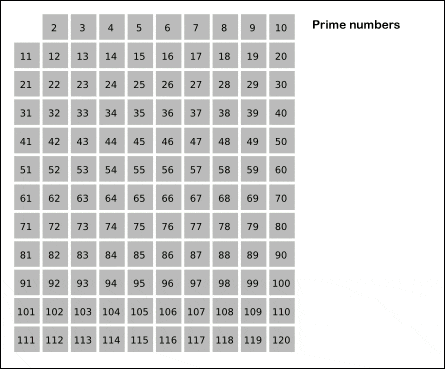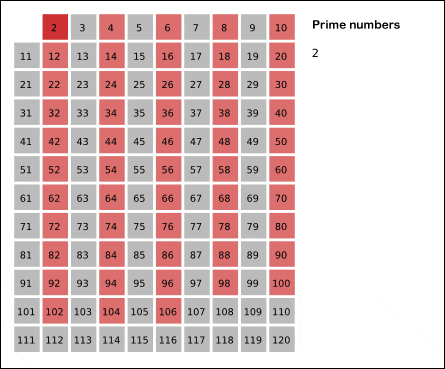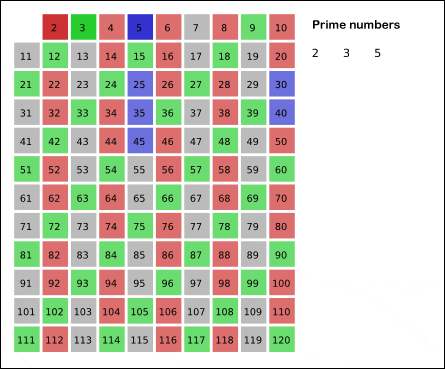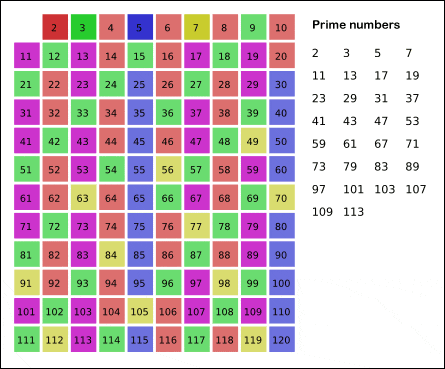
First we write down all numbers, then we "remove" all numbers that are dividable by 2 (except 2 itself). Then we do the same with 3. 4 is already removed, so the next one is 5... And in the end, all numbers left are prime.

So how does that look like in PicoLisp? First, we create a list of all numbers with range. Then we set all numbers to NIL that are not prime, and as last step, we filter the list for all non-NIL values.

Let's go: First we define the list and set the first number, 1, to NIL because 1 is not prime.

(de sieve (N)
   (let Sieve (range 1 N)
      (set Sieve)

set Sieve is equal to set Sieve NIL, which sets the val of the list to zero. (If this is unexpected, read here about the set function).

Then we check the remaining list (cdr Sieve). For each number n in the list, we "remove" the n'th element. An elegant way to implement this is using the "third form of the for loop", a construct that we have already seen for example in the Rosetta Code 100 Doors task:

define a "temporary sieve" S and loop over it: (for (S ... S ...))
in each loop, the temporary sieve S is a list starting from the I^2 position: (nth Sieve (* I I)), for example (4, 5, 6, 7...) for I=2.
Next, we shorten the list by "jumping"I elements until the list is empty ((4, 6, ...), (6, 8, ...)): (nth (cdr S) I).
Each time we do that, we set the first list element to NIL with set.

(for I (cdr Sieve)
   (when I
      (for (S (nth Sieve (* I I)) S (nth (cdr S) I))
         (set S) ) ) )

As last step, all we need to do is to filter all non-NIL values:

(filter bool Sieve)

This is the finished program:

(de sieve (N)
   (let Sieve (range 1 N)
      (set Sieve)
      (for I (cdr Sieve)
         (when I
            (for (S (nth Sieve (* I I)) S (nth (cdr S) I))
               (set S) ) ) )
      (filter bool Sieve) ) )

It outputs all prime numbers up to a given N:

: (sieve 100)
-> (2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97)

Efficiency considerations

Our new function performs much better than the previous one, but still not good enough - N=10000 already takes up to a minute. Why is that? Instead of truly "removing" items, we just set them to NIL, but they are still included in each list operation.

In order to improve the speed, we should try to remove the non-prime elements instead of flagging them as NIL. Here we go:

Improvements: Rolling the "Wheel"

Now we use a trick that we have already seen this in the Euler Task 3.

Note: The following code is based on the Rosetta Code.

The idea is that we can get a list without any multiples of 2, 3, 5 and 7, if we continuously add up this circular list:

(setq WHEEL-2357
    (2  4  2  4  6  2  6  4
     2  4  6  6  2  6  4  2
     6  4  6  8  4  2  4  2
     4  8  6  4  6  2  4  6
     2  6  6  4  2  4  6  2
     6  4  2  4  2 10  2 10 .))

It works like this: We start with N=11 (because this is the first prime number not covered).

N = N+2 = 13
N = 13+4 = 17
N = 17+2 = 19
N = 19+4 = 23
N = 23+6 = 29
...

We receive a list that effectively removes all multiples of 2, 3, 5 and 7. Defined as function:

(de roll2357wheel (Limit)
    (let W WHEEL-2357
        (make
            (for (N 11  (<= N Limit)  (+ N (pop 'W)))
                (link N)))))

Test it:

: (roll2357wheel 100)
-> (11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97)

Removing all multiples

The main issue with our previous approach was that we never removed multiple items - we just flagged them to NIL. Therefore we had many operations on the list that were actually not needed. Let's see how we can improve this.

First we can now define our wrapping function sieve. In the first step, we create a list of numbers excluding multiples of 2, 3, 5 and 7.

(de sieve (Limit)
    (let Sieve (roll2357wheel Limit)

Then we call a function remove-multiples (still to be defined), that removes the multiples of each list element destructively. We could call it for each list element, but actually we only need to go up to sqrt Limit (because the largest possible divisor is the root of Limit).

(for (P Sieve  (<= (car P) (sqrt Limit))  (cdr P))
   (remove-multiples P))

Now the tricky part: We traverse through our list and remove the multiples for each element. I. e., first we remove all multiples of 11 (starting from 121, then 132, 143...), then multiples of 13, 17 and 19 so on. Each time, we want to operate on the Sieve list directly to keep it efficient.

This is how we define remove-multiples:

We take the first element of L and move up to the list until we find the first multiple M, which is N*N (there are no multiples below that because those should already be removed).

In order to move through the list, we use two pointers: the "original" pointer L and a second pointer Q which is set to (cdr L). These pointers are incremented by one in each step until (cdr L) is NIL:

(de remove-multiples (L)
   (let (N (car L)  M (* N N))
      (for (Q (cdr L) Q (cdr (setq L Q)))

Example: if our list is L=(11, 13, 17, 19...), i. e. N=11, M=121. First iteration: L points to 11 and Q points to 13, 2nd iteration: L=13, Q=17, 3rd iteration: L=17, Q=19....

Now we move up until we "hit" our first multiple Q=M. If this is the case, we "cut" M out of our list. We can do this with con, which connects the first element of L (which is one element prior to Q) to a second list. In order to skip M, we connect L to cdr Q:

(when (= (car Q) M)
   (con L (cdr Q)) )

con is a destructive operation, i. e. the pointer from the CAR of L to M is lost forever.

Note that cdr is not destructive. Therefore all elements prior to that cutting step are not damaged, because we keep a pointer to the original list in our main function.

Now that we removed one multiple, we need to increase M by N:

(when (> (car Q) M)
   (inc 'M N) )

Since some multiples might already be removed (for example 11x12 is already removed as multiple of "2"), we actually need to check this before the (= (car Q) M) condition. So this is the final code of remove-multiples:

(de remove-multiples (L)
   (let (N (car L)  M (* N N))
      (for (Q (cdr L) Q (cdr (setq L Q)))
         (when (> (car Q) M)
            (inc 'M N) )
         (when (= (car Q) M)
            (con L (cdr Q)) ) ) ) )

Note that this function has no return value as it modifies L directly.

Now we're almost done. All we need to do is to add 2, 3, 5, 7 to our prime numbers list, because our Sieve list started from 11. This is the final function:

(de sieve (Limit)
    (let Sieve (roll2357wheel Limit)
        (for (P Sieve  (<= (car P) (sqrt Limit))  (cdr P))
            (remove-multiples P))
        (append (2 3 5 7) Sieve)))

Get the 10001st prime number

The density of prime numbers is roughly logarithmic. So the easiest approach to get the 10.001st number is to aim for a number around 100.000 and manually increase if needed, until we get a 10.001st list element:

: (nth (sieve 100000) 10001 1)
-> NIL
: (nth (sieve 110000) 10001 1)
-> 104743

The final code can be downloaded here: