Riddle 3: Largest Prime Factor

Let's start the new PicoLisp Year 2022 with a little warm-up: The third task from the Project Euler which is a rather easy, but yet interesting challenge.

Task description

The prime factors of 13195 are 5, 7, 13 and 29. What is the largest prime factor of the number 600851475143 ?

Some words about integer factorization

Until today, no efficient algorithm for integer factorization is known, leaving only heuristic and brute-force solutions to get the prime factors of large numbers. What are "large numbers"?

In February 2020, a 250 decimal digits number* was successfully factorized by a French Team with help of approx. 2700 CPU core years (reference: a 2.1GHz Intel Xeon Gold 6130 CPU). The next largest number with 260 decimal digits has not been cracked yet: en.wikipedia.org/wiki/RSA_Factoring_Challenge.

Compared to that, a 12 digits number like in our task can hardly be considered as "large number". So, brute force algorithms might actually work.

A brute force solution using prime number lists

What do we know about the factors of a number N?

The smallest possible factor is 2.
The largest possible factor is the square root, (sqrt N).
All factors are prime numbers.

With this knowledge, we could utilize an existing list of prime numbers and try all numbers inside that list. The square root is 775146.1, and after some research we can find that there are exactly 62113 prime numbers smaller than that (according to this resource. There are lists for that purpose ready for download, for example this one: primes.utm.edu/lists/small/100000.txt.

In short, when using a pre-fabricated list, we can determine after max. 62113 calculations if N can be factorized or not.

Heuristic approaches to get prime factors

Now let's assume we find it boring to use a pre-fabricated list. Here is how we can find it using heuristic methods. We define a function factor that takes an integer N as argument and returns a list of all prime factors. For example, for 12 it returns 2 2 3.

Let's try to sketch the basic algorithm as described in Donald Knuth's "The Art of Computer Programming, Vol. 2":

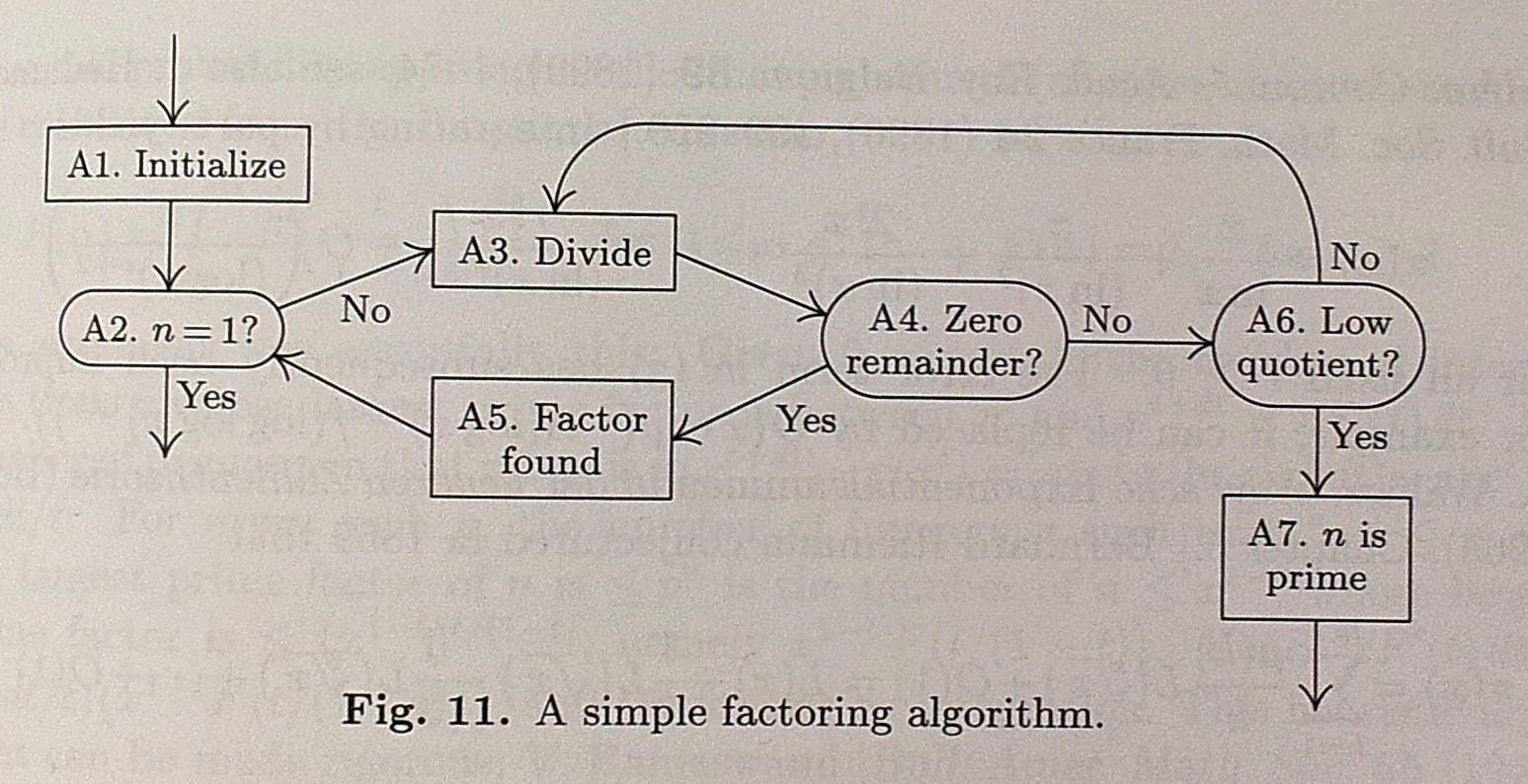
Let's translate to PicoLisp.

A1: Initialize - (let (D 2 M (sqrt N)), where D is the divisor and M is its maximum value.
A2: n=1?: (while (> N 1))
A3: Divide: (% N D)
A4: Zero Remainder?: (if (=0 (% N D))
A5: Factor found:
- redefine N: (setq N (/ N D))
- redefine M: (setq M (sqrt N))
- add D to result list: (make ... (link D))
**A6. Low quotient:increase divisor, if possible:(inc D)``
**A7. n is prime: Add n to list with (link N).

In total, it looks like this:

(de factor (N)
   (make
      (let (D 2 M (sqrt N))
         (while (> N 1)
            (if (=0 (% N D))
               (setq M (sqrt (setq N (/ N (link D)))))
               (inc 'D) ) ) ) ) )

Let's add a further improvement. If N is prime, we won't reach the exit condition (while (> N 1)) until D=N. However, we know that the maximum divisor is equal to the square root of N, or N is prime. So let's replace the while-condition > N 1 by >= M D.

...
      (let (D 2 M (sqrt N))
         (while (>= M D)
...

For example, let's calculate (factor 12).

Initialization: N=12, D=2, M=3 (PicoLisp calculations are all integers, so no need to worry about rounding errors).
First iteration: We find that 12 can be divided by 2. So we store 2 in our results list and set N=6 and M=2. Then we divide again and get N=3 and M=1.
Second iteration: We increase D by one and can again divide. So we store D in our list and set N=1 and M=1. With this, we reach the exit condition and are done.

This was very fast because 12 has a lot of divisors. However in worst case - if N is prime - we need sqrt(N)-1 calculation steps. This can certainly be improved.

Some optimization: Circular lists

In our current solution, D takes every value from 2 to sqrt(N) max. However we have a lot of redundancy here, because of course these numbers are not all prime. For example, we know that all prime numbers >2 are odd. This means, instead of incrementing D by 1, we can increment it by 2 after we the first iteration step: 2, 3, 5, 7, 9, 11, ...

There are a number of ways to do that. One possibility is to define if conditions or similar. But there is a more elegant way using the following circular list:

(let L (1 . (2 .))

Circular lists are formed by a dot . as last element which sets the pointer back to the first element. In other words, we get the following cell structure:

+-----+-----+     +-----+-----+     
|  1  |  ---+---->|  2  |  |  +
+-----+-----+     +-----+-----+     
                     ^     |
                     |     |
                     +-----+

Note: The dot . in (1 . is not for circularity but to create a dotted pair. This makes sure that the second list's items are not a sublist of the first list, but on the same hierarchy level. Otherwise we would get a structure like this, and pop would return the circular sublist instead of single items:

+-----+-----+     +-----+-----+
|  1  |  ---+---->|  |  |  /  |
+-----+-----+     +--+--+-----+
                     |
                     v
                  +-----+-----+     
                  |  2  |  |  +
                  +-----+-----+     
                     ^     |
                     |     |
                     +-----+

Getting elements with `pop`

In order to rotate through the circular list and get the items one after another (in an infinite loop), we can use pop. You can read more about pop in the previous article..

: (setq L2 (1 2 3 4 .))
-> (1 2 3 4 .)
: (pop 'L2)
-> 1
: L2                   
-> (2 3 4 1 .)

Let's apply this idea to our prime factorization program: We add a list L with the incremented values, and increment D accordingly:

...
   (let (D 2 M (sqrt N) L (1 . ( 2 .)))
      ...
      (inc 'D (pop 'L) ) )

This increments D by 1 in the first loop and by 2 ever after. Effectively this cuts down the number of calculations by approx. 50%.

Instead of pop 'L, we can also write ++ L (slightly more efficient due to the missing quote).

Removing multiples of `3` and `5`

With the same approach, we can also take out all multiples of 3. From our current list (2, 3, 5, 7, 9, 11, 13, ...) we can take out (6, 9, 12 ...). This corresponds to "jumping" every third factor. Achieving this is simple - we only need to modify the circular part of L.

(let L ( 1 2 . ( 2 4 .))

returns 3, 5 in the linear part and then 7, 11, 9, 13, ... in the circular part. This improves efficiency by another 16%, as we remove 1/6 of all factors.

Now our factor list looks like this: (2, 3, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31, 35)... Obviously we can also take out 25, 35, 55, 65... and so on, as these are already "covered" by 5.

The required circular list is slightly more complicated but still easy to calculate by hand:

(let L (1 2 2 . (4 2 4 2 4 6 2 6 .))

Now we could also exclude multiples of 7, 11, 13 and so on, but it is not really needed for our small Euler task.

This is the final code:

(de factor (N)
   (make
      (let (D 2  L (1 2 2 . (4 2 4 2 4 6 2 6 .))  M (sqrt N))
         (while (>= M D)
            (if (=0 (% N D))
               (setq M (sqrt (setq N (/ N (link D)))))
               (inc 'D (++ L)) ) )
         (link N) ) ) )

(printsp (factor 600851475143))

Benchmarking

Now just for fun, let's benchmark the algorithm with some worst-case scenarios (i. e. N is prime). My notebook's CPU is a AMD Ryzen 5 3500 U, so not a particularly fast one.

9 digits (60862019): 0.000 sec
10 digits (608527279): 0.001 sec
11 digits (6085160639): 0.003 sec
12 digits (60085163279): 0.009 sec
13 digits (600085179017): 0.020 sec
100 digits (RSA-100 challenge, first cracked in 1991): no result after 2 hours.

So this is certainly not the algorithm of choice if you plan to crack encrypted messages, not even those that are considered outdated since 30 years.

You can find the finished program here.

Sources

projecteuler.net/problem=3
rosettacode.org/wiki/Prime_decomposition#Pi..
Donald Knuth: The Art of Computer Programming, Vol. 2
software-lab.de/doc/index.html