The Task
The sum of the squares of the first ten natural numbers is,
1^2 + 2^2 + 3^3 + ... + 10^2 = 385
The square of the sum of the first ten natural numbers is,
(1 + 2 + 3 + ... + 10)^2 = 55^2 = 3025Hence the difference between the sum of the squares of the first ten natural numbers and the square of the sum is:
3025 - 385 = 2840Find the difference between the sum of the squares of the first one hundred natural numbers and the square of the sum.
There are three solutions to this task:
- A straightforward one -> 14 lines
- A functional, "lispy" one -> 3 lines
- A mathematical one -> 2 lines.
The straightfoward solution
This one is very simple, because we just do literally what is in the task description. We have three functions: sum_squared, which sums up and squares the result, squares_sum, which forms the square and then sums up, and task_6 which combines it to deliver the solution.
(de sum_squared (N)
(let Sum 0
(for I N
(inc 'Sum I) )
(* Sum Sum)) )
(de squares_sum (N)
(let Sum 0
(for I N
(inc 'Sum (* I I)) )
Sum ) )
(de task_6 (N)
(-
(sum_squared N)
(squares_sum N)) )
The functional solution
The code above smells a little bit like repetition and redundancy. Redundant tasks in sum_squared and squares_sum:
- In both functions, we use a helper variable
Ito sum up from 0 to N. - in both functions, we increment a variable
Sum.
Let's first try to improve the first point. Instead of for I N, we could use a list, because we all know that PicoLisp has powerful list functions. With range, we can create a list from 1 to N.
: (setq L (range 1 10))
-> (1 2 3 4 5 6 7 8 9 10)
Next, we can use apply to apply the + function to all elements on the list.
: (apply + L)
-> 55
This is equivalent to the first 4 lines of our sum_squared function above.
In the same way, we can use the sum function to apply the * function to each element of a list and return the numerical sum of the list elements. The syntax is (sum 'fun 'lst ...):
: (sum * L L)
-> 385
This single line is equivalent to our squares_sum function.
In other words, the above code can be shortened down to:
(de task_6 (N)
(let (L (range 1 N) S (apply + L))
(- (* S S) (sum * L L)) ) )
Note: Depending on the usecase, you need to cosnider that the apply function requires a lot of stack space. If you have the latest PicoLisp version installed, you will get a "stack overflow" error message if the numbers get too large.
: (task_6 100000)
-> 25000166664166650000
: (task_6 1000000)
!? (apply + L)
Stack overflow
The mathematical approach
Now, the "lispy" solution already has many improvements, such as reducing redundancy and repetition. However, internally we still have a lot of looping and iteration going on, which causes some (potential) limitations on the applicable range - depending on the use case of course. So let's look for mathematical approaches to improve our solution further.
There is a famous story about young Gauss who allegedly finished the teacher's task to sum up all numbers from 1 to 100 within minutes. He did that with the so-called "Gaussian Sum Formula":
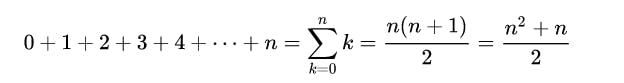
Accordingly, the square of the sum can be expressed as ((n^2 + n)/2 )^2).
In order to find the sum of squares, we can use the formula for square pyramidal numbers:
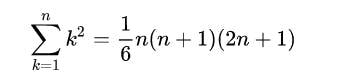
Now we bring these two formulas together, extract n and re-group the factors a little bit to make it more pretty. With some easy calculations, you can form it to the following identity:
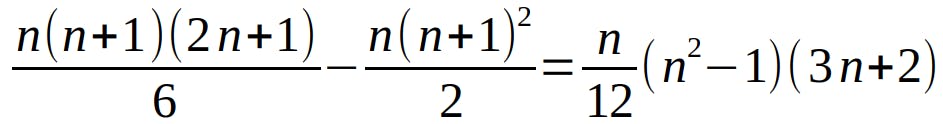
In PicoLisp:
(de task_6 (N)
(/ ( * N (- (* N N) 1) (+ (* 3 N) 2)) 12) )
This solution don't needs any loops or iterations, which means that the computation time will stay almost constant.
You can find the source code of the examples here:

