In the last post, we have seen how we can create a knowledge base and run queries on it. Today we will try to understand how Prolog computes the result of a query.
This chapter is based on this Prolog tutorial.
What is Unification?
Let's check the definition for unification:
Two terms unify if they are the same term or if they contain variables that can be uniformly instantiated with terms in such a way that the resulting terms are equal.
Sounds complicated, let's check it step by step. "Two terms unify if they are the same term". That is actually trivial. We can test that with the built-in predicate equal/2 (/2 means that the predicate takes two arguments):
: (? (equal John John))
-> T
: (? (equal John Susie))
-> NIL
Let's define a knowledge base as follows:
(be house_elf (Dobby))
(be witch (Hermione))
(be witch (Rita_Skeeter))
(be wizard (Harry))
(be magic (@X)
(or
((house_elf @X))
((wizard @X))
((witch @X)) ) )
We open the knowledge base with pil magic.l + in the REPL. Now we can write a query for magic. The defined rule says that magic is true if @X is either a house_elf, a wizard or a witch.
: (? (magic @X))
@X=Dobby
@X=Harry
@X=Hermione
@X=Rita_Skeeter
-> NIL
From the output above we can see that @X unifies with with Dobby, Harry, Hermione and Rita_skeeter. To understand what is happening, let's use some additional tracing features of pilog.
First of all, we can check the defined rules with the rules function:
: (rules 'magic)
1 (be magic (@X) (or ((house_elf @X)) ((wizard @X)) ((witch @X))))
-> magic
We see that in this case there is only one rule for magic, with three subclauses which are connected by or. Now let's trace it using (? <predicate(s)> ( <predicate> <arg1> ...)):
: (? magic house_elf wizard witch (magic @X))
1 (magic @X)
1 (house_elf Dobby)
@X=Dobby
1 (wizard Harry)
@X=Harry
1 (witch Hermione)
@X=Hermione
2 (witch Rita_Skeeter)
@X=Rita_Skeeter
With this we are tracing the predicates magic, house_elf, wizard and witch. We see that magic only appears at the very beginning, after that the other predicates are executed. Pilog tries to unify @Xwith the first known fact which is defined in the house_elf predicate, which returns Dobby. Thus Dobby can be unified with @X.
After that, Pilog moves on to the next predicate, wizard, and then witch.
What is happening here? Pilog is doing a backtracking tree search.
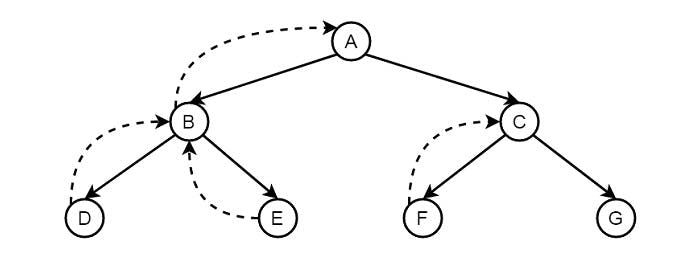
This is an important concept which we will further explore in the next post when we will talk about recursion.
Example: Crossword Puzzle
Now let's illustrate the unification process at a little more interesting example: A simple crossword puzzle for six italien words: astante, astoria, baratto, cobalto, pistola, statale. They should be arranged in the following grid:
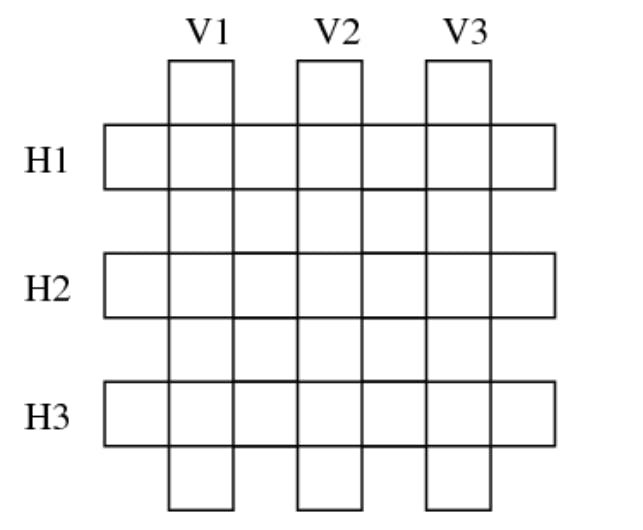
How can we solve this with help of Pilog?
First, let's define the knowledge base. We know that we have six words with seven letters each. Let's define it like this: first comes the full word, after that comes each letter as single argument.
(be word (astante a s t a n t e))
(be word (astoria a s t o r i a))
(be word (baratto b a r a t t o))
(be word (cobalto c o b a l t o))
(be word (pistola p i s t o l a))
(be word (statale s t a t a l e))
Now we can define the rule for our crossword. Let's start with the left half of the clause: we want a valid crossword solution with six words @V1-3, @H1-3.
(be crossword (@V1 @V2 @V3 @H1 @H2 @H3)
Basically we have only one rule: The crossword solution is valid if the letters at the intersections are identical. If you check the grid, you will agree that this means that the 2nd, 4th and 6th letter of each vertical and horizontal word must match. On the other hand, we don't care about the 1st, 3rd, 5th and 7th letter. The "don't care"-letters can be written as @ - a so-called anonymous variable.
(be crossword (@V1 @V2 @V3 @H1 @H2 @H3)
(word @H1 @ @H12V12 @ @H14V22 @ @H16V32 @)
(word @H2 @ @H22V14 @ @H24V24 @ @H26V34 @)
(word @H3 @ @H32V16 @ @H34V26 @ @H36V36 @)
(word @V1 @ @H12V12 @ @H22V14 @ @H32V16 @)
(word @V2 @ @H14V22 @ @H24V24 @ @H34V26 @)
(word @V3 @ @H16V32 @ @H26V34 @ @H36V36 @) )
where @H12V12 is the second letter of the first horizontal and first vertical word, @H14V22 is the fourth letter of the first horizontal and the second letter of the second vertical word, and so on.
Now we can feed this to Pilog and query the solution. We get six valid results:
: (? (crossword @V1 @V2 @V3 @H1 @H2 @H3))
@V1=astante @V2=baratto @V3=statale @H1=astante @H2=baratto @H3=statale
@V1=astoria @V2=baratto @V3=statale @H1=astante @H2=cobalto @H3=pistola
@V1=astante @V2=cobalto @V3=pistola @H1=astoria @H2=baratto @H3=statale
@V1=astoria @V2=cobalto @V3=pistola @H1=astoria @H2=cobalto @H3=pistola
@V1=baratto @V2=baratto @V3=statale @H1=baratto @H2=baratto @H3=statale
@V1=cobalto @V2=baratto @V3=statale @H1=cobalto @H2=baratto @H3=statale
-> NIL
Solution 1, 4, 5 and 6 contain duplicates, but solution 2 and 3 are unique (feel free to implement a filter to test for unique solutions).
I think this example illustrates the power of Pilog in a very nice way: You just need to feed in the facts and the desired target, and you can get all solutions instantely without caring too much about what is happening internally.
You can find the knowledge base magic.l and crossword.l here.
In the next post we will go deeper into recursion, one of the most important concepts in Pilog/Prolog.
Sources
let.rug.nl/bos/lpn//lpnpage.php?pagetype=ht..
tutorialspoint.com/prolog/prolog_backtracki..
github.com/dragonwasrobot/learn-prolog-now-..

