Welcome back to the second part of the "Binary tree traversal" task from Rosetta Code. This is a follow up to part 1.
We have solved everything except for the level-order traversal.
The level-order traversal
As a reminder, we are looking at the following tree:
1
/ \
/ \
/ \
2 3
/ \ /
4 5 6
/ / \
7 8 9
What we want to get is the output from top to bottom and left to right: 1 2 3 4 5 6 7 8 9. This means that we will visit each level and get the output.
Yesterday we discussed the fifo function as a little preparation for solving this task. The fifo function allows us to create a queue from which we always take out the oldest item.
Creating the queue
But what are our queue items?
- At first, we only have one item in the queue: The full tree.
- Then we take the tree root, which means we have two trees left: The left and right tree. These are put in the waiting queue.
- Then we take out the first tree in the queue and take the root.
- Again, we queue up its left and right trees.
- And so on.
In the animation below, you can get an impression how the algorithm works.
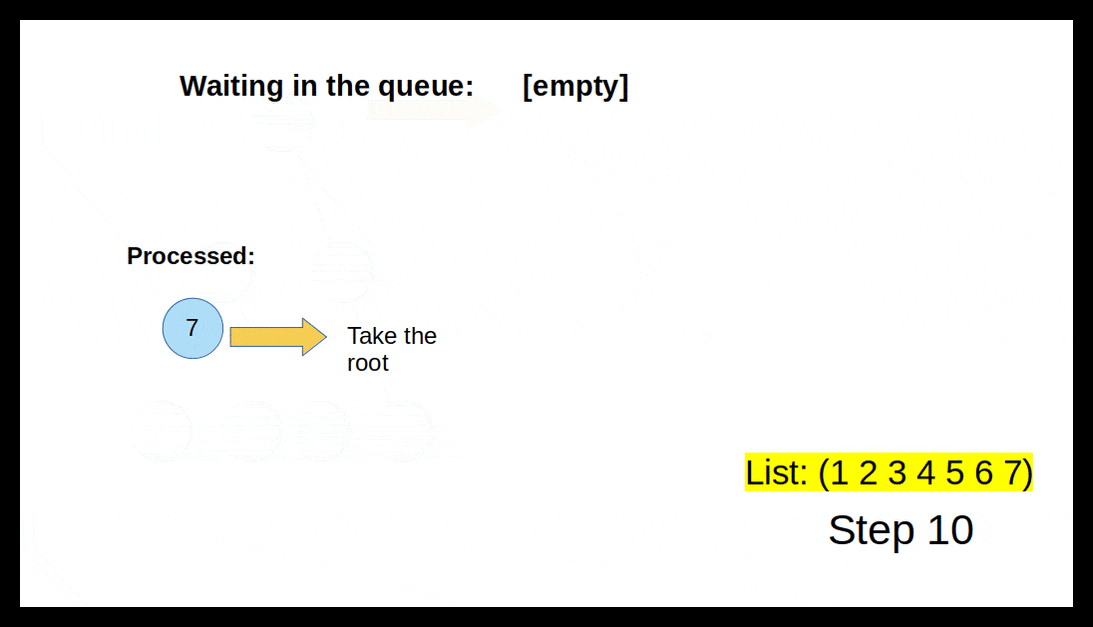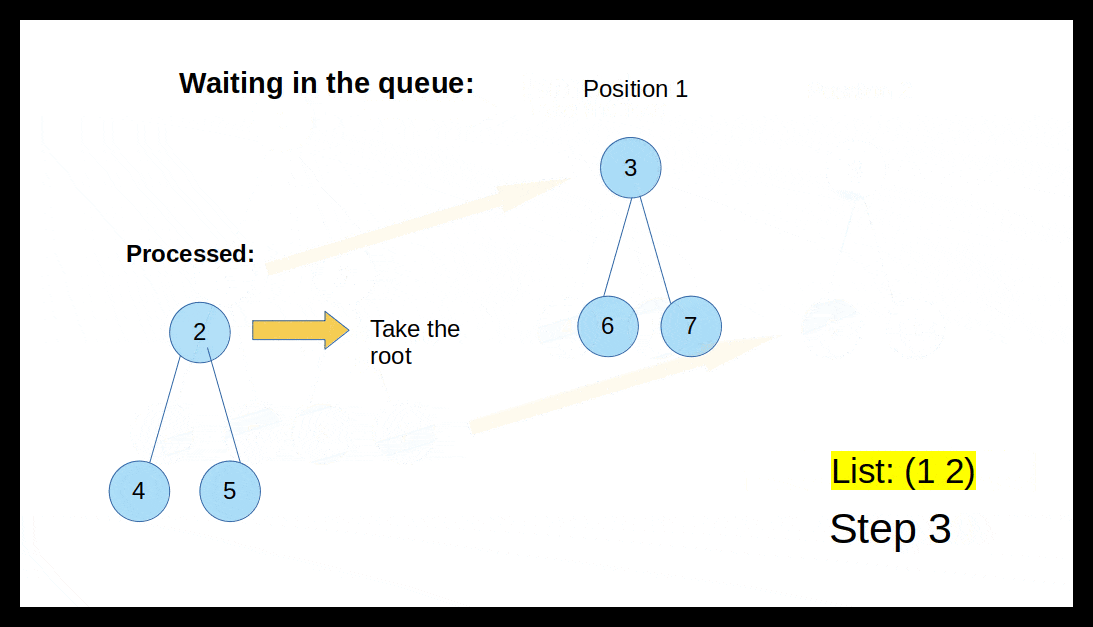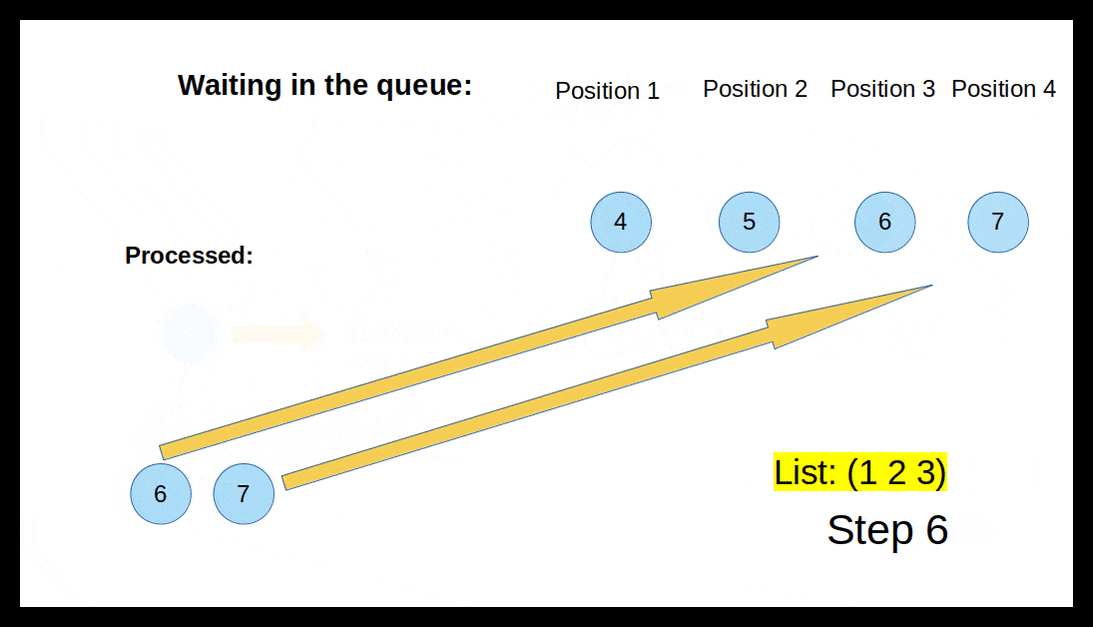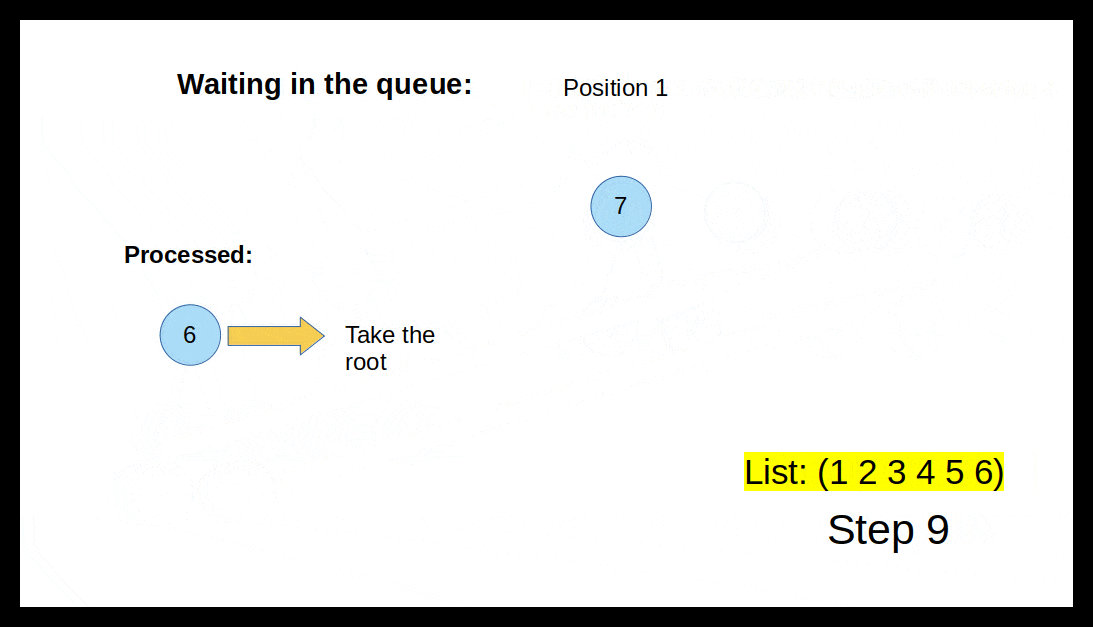
Unfortunately, this time it is easier to draw it on paper than to write it as code. Let's try. Reminder: We can get the left subtree with (cadr *Tree) and the right subtree with caddr *Tree.
The first round
We know that we want to put our binary tree into a fifo list. A fifo list is circular. In order to use the fifo function, we need a variable to store our queue. So let's define a variable Q (like "queue") and store the queued items there. We can make it circular with the circ function.
In the beginning, there is only a single item: The whole tree.
: (setq Q (circ *Tree))
-> ((1 (2 (4 (7)) (5)) (3 (6 (8) (9)))) .)
Now we can apply what we learned about the fifo function.
Let's take the first item in the queue with fifo <list> and store it in a variable N:
: (setq N (fifo 'Q))
-> (1 (2 (4 (7)) (5)) (3 (6 (8) (9))))
As expected, our fifo list only had one item which was the full tree. Now the queue is empty again.
Let's print out the root, just like we did in the recursive tree traversal functions. The node is simply the car.
(printsp (car N))
Now we want to add the left and right subtree to the queue, if they exist. The syntax for adding new items to a fifo list is fifo <list> <item>.
The existence check and subsequent adding can be written like this:
(when (cadr N) (fifo 'Q @))
(when (caddr N) (fifo 'Q @)) ) ) )
@ is a short symbol for the result of the conditional
expression when we evaluate flow functions. We could have as well written (cadr N) and (caddr N).
Now we have two new items in the queue: the left subtree and right subtree. What next?
...and the rest
This is what we have now in our queue:
: Q
-> ((3 (6 (8) (9))) (2 (4 (7)) (5)) .)
So what we basically need is a so-calledfor loop that runs until Q is empty. If you followed the previous posts carefully, this might remind you of the "100 Doors" task, where we had a similar topic (= executing our actions as long as the "Doors"-list was not empty).
In this case, we used the "third form of the for loop" (check the docs), which takes three parameters: A symbol that we use in the loop, a list to which this symbol is bound, and an exit condition. The loop is executed as long as the exit condition is non-NIL.
So let's bound Q to the circular Tree-List. The loop should stop when Q is NIL. Like this:
(for (Q (circ Tree) Q)
Now we just have to put it together:
(de level-order (Tree)
(for (Q (circ Tree) Q)
(let N (fifo 'Q)
(printsp (car N))
(when (cadr N) (fifo 'Q @))
(when (caddr N) (fifo 'Q @)) ) ) )
We call it and get (level-order: 1 2 3 4 5 6 7 8 9). Finished!
The final code can be downloaded here.

